Composite-Tutorial                           Remember to Bookmark This Page

 Tutorial Video

 

Enter Composite Fiber and Matrix Properties:

Modulus of the Fiber,     E_f     Pa     

Modulus of the Matrix,      E_m  Pa

Shear Modulus of the Fiber,     G_f    Pa      

Shear Modulus of the Matrix,     G_m    Pa 

Poisson's Ratio of the Fiber,    ν_f 

Poisson's Ratio of the Matrix,    ν_m        

Density of the Fiber,      ρ_f  kg/m3

Density of the Matrix,    ρ_m kg/m3

Fiber Volume Fraction,  V   

 

Enter Physical Properties of Laminate

Number of layers,  n

Layer Thickness,  t    m

Length,   L    m

Base, b    m

Ply Angle From Top to Bottom (For less # of Layers Leave Blank Boxes)

Ply angle of Layer 1   Degrees

Ply angle of Layer 2   Degrees

Ply angle of Layer 3   Degrees

Ply angle of Layer 4   Degrees

Ply angle of Layer 5   Degrees

Ply angle of Layer 6   Degrees

Ply angle of Layer 7   Degrees

Ply angle of Layer 8   Degrees

Ply angle of Layer 9   Degrees

Ply angle of Layer 10   Degrees

 

Assuming chordwise rigid, theses rigidities are only valid for unidirectional unbalanced stacking or symmetric stacking sequences.

Effective Bending Rigidity "EI"

Effective Torsional Rigidity "GJ"

Effective Coupled Bending-Torsion Rigidity "K"

 

 

The following Matrices are Valid for any Stacking Sequence

For reference:

Bending Stiffness

D(1,1) D(1,2) D(1,3)

D(2,1) D(2,2) D(2,3)

D(3,1) D(3,2) D(3,3)

 

Extensional Stiffness

A(1,1) A(1,2) A(1,3)

A(2,1) A(2,2) A(2,3)

A(3,1) A(3,2) A(3,3)

 

Coupling Stiffness

B(1,1) B(1,2) B(1,3)

B(2,1) B(2,2) B(2,3)

B(3,1) B(3,2) B(3,3)

 

 

 

Calculating Effective Rigidities of a Laminated Composite Beam (Classical Laminate Theory)

 

 Introduction

The application of fibre-reinforced composite materials in the aerospace industry extends from commercial to military aircraft, such as the Boeing F18, B2 Stealth Bomber, AV-8B Harrier (Jones, 1998). The attractiveness of composites lies in their mechanical properties; such as weight, strength, stiffness, corrosion resistance, fatigue life. Composites are widely used for control surfaces such as ailerons, flaps, stabilizers, rudders, as well as rotary and fixed wings. That is why the analysis of composite structures is imperative for aerospace industry. The main advantage of composites is their flexibility in design. Mechanical properties of the laminate can be altered simply by changing the stacking sequence, fibre lay-up and thickness of each ply which leads to optimization in a design process. 

 

Assumptions 

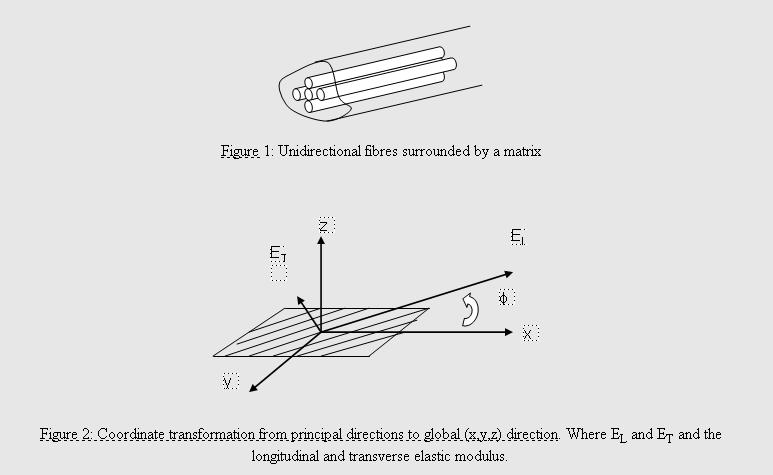
The composite beam is modeled based on the chord-wise bending moment (about the z-axis) being small compared to the span-wise moment (about the y axis, see Figure 2). The chord-wise moment is then neglected. The composite material pertaining to this research is a unidirectional fibre reinforced composite material. The given information of any unidirectional composite material is the elastic modulus in both the longitudinal and transverse axis (see Figures 1 and 2), Poison’s ratio and the shear modulus in the principle directions.

 

 

 

Effective rigidities for a solid cross-section

 

The reduced stiffness constants in the material principle directions are:

 

 

where T  is the transformation matrix which is used to transform the reduced stiffness constants from the principal material fibre directions to a global (x, y, z) beam coordinates.

Then, the resulting transformed reduced stiffness constants for a unidirectional or orthotropic composite from its principal directions is (Berthelot, 1999):

 

     Both equations (above) can be merged into a single equation commonly known as the “Constitutive Equation”. The constitutive equation describes the stiffness matrix of a laminate plate. The resultant forces and moments are functions of the in-plane strains and curvatures (Berthelot, 1999).

  

where  is the distance from the mid-plane of the laminate (Figure 3).

 .

     For a bending-torsion coupling behaviour the chord wise moment Mx is assumed to be zero so that the kx curvature can be eliminated from (above) and then the matrix  equation (11) reduces to the following form:

 

 

where,

 

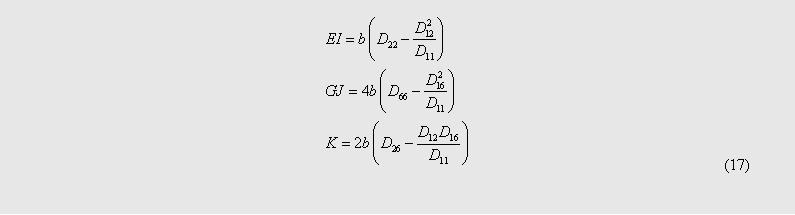
     The EI, GJ and K represent the effective rigidities of the beam in the global (x, y, z) coordinate system. EI, GJ, and K represent, respectively, the bending rigidity, torsion rigidity and bending-torsion coupled rigidity. The effective rigidities are functions of ply angle, thickness, and stacking sequence.